Voici la meilleure façon de découper une pizza (selon la science)

Décidément, les scientifiques sont de gros gourmands. Alors qu'en mars 2015, un mathématicien expliquait pourquoi il ne faut jamais couper un gâteau en parts triangulaires, deux chercheurs de l'Université de Liverpool viennent de remettre ça - mais en s'intéressant cette fois-ci à la pizza.

Pour la plupart des êtres humains normalement constitués, une pizza parfaite est un savant mélange de pâte croustillante (et fine pour les puristes), de fromage fondu et de sauce tomate. La découpe elle, n'a que peu d'importance. Mais c'était sans compter sur Joel Haddley et Stephen Worsley, deux mathématiciens gourmets et hautement minutieux, qui se sont demandés comment découper une pizza en parts exactement égales.

Et le résultat est loin de correspondre à nos habituelles parts triangulaires. En utilisant la géométrie, les mathématiciens ont découpé leur pizza sous forme de rosace. Au total, la pizza compte 12 parts.

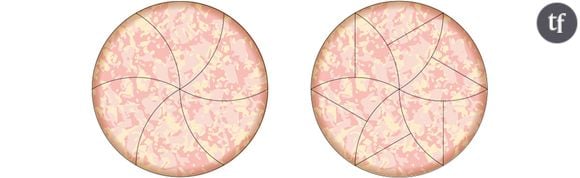
Mais si les morceaux sont égaux en termes de proportionnalité, ils sont loin de l'être en termes de garnitures ! En effet, si les parts du milieu sont extra fondantes, celles qui les complètent comportent ont forcément de la croûte. Alors certes, il y a deux écoles : les mangeurs de croûtes et ceux qui l'abandonnent lâchement dans le carton à pizza, mais cette découpe - aussi exacte qu'elle soit - ne semble pas très fair-play.

On ne s'avancera pas trop en disant que cette technique de découpage ne sera jamais utilisée par personne. Mais bien essayé les gars.